회귀란?
회귀(Regression)분석은 데이터 값이 평균과 같은 일정한 값으로 돌아가려는 경향을 이용한 통계학 기법입니다. 통계학 용어를 빌리자면 회귀는 여러 개의 독립변수와 한 개의 종속변수 간의 상관관계를 모델링하는 기법을 통칭합니다.
독립변수의 값에 영향을 미치는 회귀 계수(Regression Coefficients)입니다. 머신 러닝 관점에서 보면 독립변수는 피처에 해당되며 종속변수는 결정 값입니다. 머신러닝 회귀 예측의 핵심은 주어진 피처와 결정 값 데이터 기반에서 학습을 통해 최적의 회귀 계수를 찾아내는 것입니다.
회귀 계수가 선형이냐 아니냐에 따라 선형 회귀와 비선형 회귀로 나눌 수 있습니다. 그리고 독립변수의 개수가 한 개인지 여러 개인지에 따라 단일 회귀, 다중 회귀로 나뉩니다.
지도학습은 두 가지 유형으로 나뉘는데, 바로 분류와 회귀입니다. 이 두 가지 기법의 가장 큰 차이는 분류는 예측값이 카테고리와 같은 이산형 클래스 값이고 회귀는 연속형 숫자 값이라는 것입니다.
여러 가지 회귀 중에서 선형 회귀가 가장 많이 사용됩니다. 선형 회귀는 실제 값과 예측값의 차이를 최소화하는 직선형 회귀선을 최적화하는 방식입니다. 선형 회귀 모델은 규제(Regulariazation) 방법에 따라 다시 별도의 유형으로 나뉠 수 있습니다. 규제는 일반적인 선형 회귀의 과적합 문제를 해결하기 위해서 회귀 계수에 페널티 값을 적용하는 것을 말합니다. 대표적인 선형 회귀 모델은 다음과 같습니다.
- 일반 선형 회귀: 예측값과 실제 값의 RSS(Residual Sum of Squares)를 최소화할 수 있도록 회귀 계수를 최적화하며, 규제(Regularization)를 적용하지 않은 모델입니다.
- 릿지(Ridge): 릿지 회귀는 선형 회귀에 L2규제를 추가한 회귀 모델입니다. 릿지 회귀는 L2규제를 적용하는데, L2규제는 상대적으로 큰 회귀 계수 값의 예측 영향도를 감소시키기 위해서 회귀 계수값을 더 작게 만드는 규제 모델입니다.
- 라쏘(Lasso): 라쏘 회귀는 선형 회귀에 L1규제를 적용한 방식입니다. L2규제가 회귀 계수 값의 크기를 줄이는 데 반해, L1규제는 예측 영향력이 작은 피처의 회귀 계수를 0으로 만들어 회귀 예측 시 피처가 선택되지 않게 하는 것입니다. 이러한 특성 때문에 L1규제는 피처 선택 기능으로도 불립니다.
- 엘라스틱넷(ElasticNet): L2, L1규제를 함께 결합한 모델입니다. 주로 피처가 많은 데이터 세트에서 적용되며, L1규제로 피처의 개수를 줄임과 동시에 L2규제로 계수 값의 크기를 조정합니다.
- 로지스틱 회귀(Logistic Regression): 로지스틱 회귀는 회귀라는 이름이 붙어 있지만, 사실은 분류에 사용되는 선형 모델입니다. 로지스틱 회귀는 매우 강력한 분류 알고리즘입니다. 일반적으로 이진 분류뿐만 아니라 희소 영역의 분류, 예를 들어 텍스트 분류와 같은 영역에서 뛰어난 예측 성능을 보입니다.
단순 선형 회귀를 통한 회귀 이해
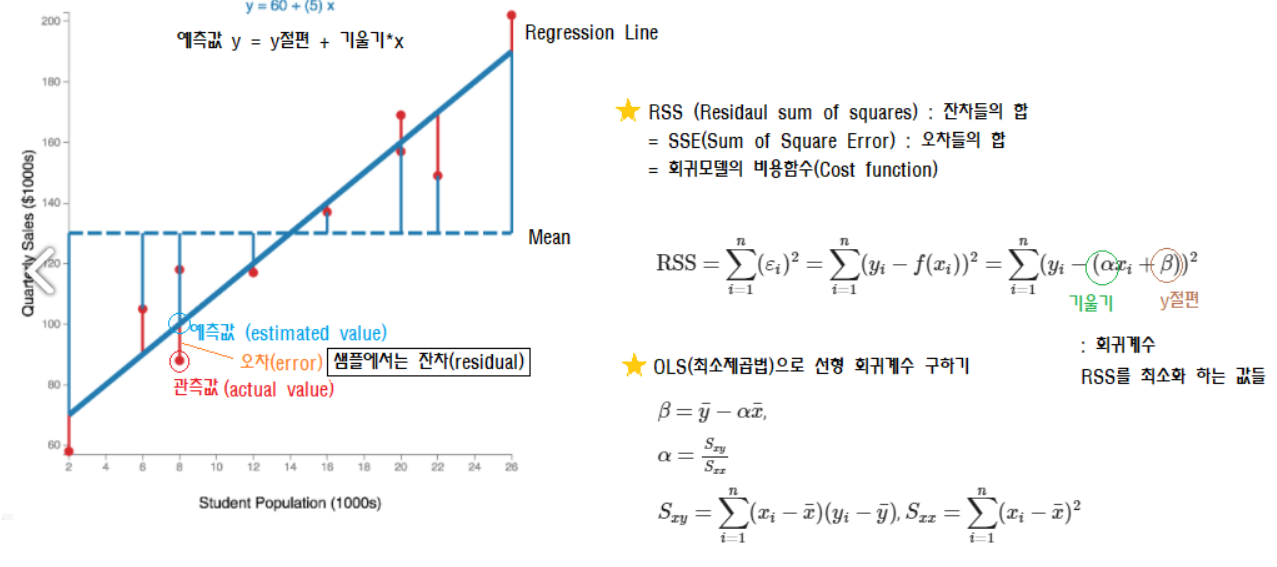
단순 선형 회귀는 독립변수도 하나, 종속변수도 하나인 선형 회귀입니다. 회귀는 실제 값과 회귀 모델의 차이에 따른 오류 값을 남은 오류, 즉 잔차라고 부릅니다. 최적의 회귀 모델을 만든다는 것은 바로 전체 데이터의 잔차(오류 값)합이 최소가 되는 모델을 만든다는 의미입니다. 동시에 오류 값 합이 최소가 될 수 있는 최적의 회귀 계수를 찾는다는 의미도 됩니다.

오류 값은 +나 -가 될 수 있습니다. 그래서 전체 데이터의 오류 합을 구하기 위해 단순히 더했다가는 뜻하지 않게 오류 합이 크게 줄어들 수 있습니다. 따라서 보통 오류 합을 계산할 때는 절댓값을 취해서 더하거나(Mean Absolute Error), 오류 값의 제곱을 구해서 더하는 방식(RSS, Residual Sum of Square)을 취합니다. 일반적으로 미분 등의 계산을 편리하게 하기 위해서 RSS방식으로 오류 합을 구합니다. 즉 Error2 = RSS입니다.
다시 말하면 RSS를 최소화하는 회귀 계수를 학습을 통해서 찾는 것이 머신러닝 회귀의 핵심 사항입니다. 독립변수나 종속변수가 아닌 w변수(회귀 계수)가 중심 변수임을 인지하는 것이 매우 중요합니다.
회귀에서 이 RSS는 비용(Cost)이며 w변수(회귀 계수)로 구성되는 RSS를 비용 함수라고 합니다. 머신러닝 회귀 알고리즘은 데이터를 계속 학습하면서 이 비용 함수가 반환하는 값을 지속해서 감소시키고 최종적으로는 더 이상 감소하지 않는 최소의 오류 값을 구하는 것입니다. 이 비용 함수를 손실함수(loss function)라고도 합니다.
비용 최소화하기 - 경사 하강법(Gradient Descent)소개
w파라미터가 많으면 고차원 방정식을 동원하더라도 해결하기가 어렵습니다. 경사 하강법은 이러한 고차원 방정식에 대한 문제를 해결해 주면서 비용 함수 RSS를 최소화하는 방법을 직관적으로 제공하는 뛰어난 방식입니다. 사실 경사 하강법은 '데이터를 기반으로 알고리즘이 스스로 학습한다'는 머신러닝의 개념을 가능하게 만들어준 핵심 기법의 하나입니다.
경사 하강법의 사전적 의미인 '점진적인 하강'이라는 뜻에서도 알 수 있듯이, '점진적으로'반복적인 계산을 통해 W파라미터 값을 업데이트하면서 오류 값이 최소가 되는 w파라미터를 구하는 방식입니다.
경사 하강법은 반복적으로 비용 함수의 반환 값, 즉 예측값과 실제값의 차이가 작아지는 방향성을 가지고 w파라미ㅓ를 지속해서 보정해 나갑니다. 최초 오류 값이 100이었다면 두 번째 오류 값은 100보다 작은 90, 세 번째는 80과 같은 방식으로 지속해서 오류를 감소시키는 방향으로 w값을 계속 업데이트해 나갑니다. 그리고 오류값이 더 이상 작아지지 않으면 그 오류 값을 최소 비용으로 판단하고 그때의 w값을 최적 파라미터로 반환합니다.
일반적으로 경사 하강법은 모든 학습 데이터에 대해 반복적으로 비용함수 최소화를 위한 값을 업데이트하기 때문에 수행 시간이 매우 오래 걸리는 단점이 있습니다. 그 때문에 실전에서는 대부분 확률적 경사 하강법을 이용합니다. 확률적 경사 하강법은 전체 입력 데이터로 w가 업데이트되는 값을 계산하는 것이 아니라 일부 데이터만 이용해 w가 업데이트디는 값을 계산하므로 경사 하강법에 비해서 빠른 속도를 보장합니다. 따라서 대용량의 데이터의 경우 대부분 확률적 경사 하강법이나 미니 배치 확률적 경사 하강법을 이용해 최적 비용함수를 도출합니다.
'Lecture ML' 카테고리의 다른 글
| 머신러닝 강좌 #27] 선형 회귀 모델을 위한 데이터 변환 (0) | 2021.07.09 |
|---|---|
| 머신러닝 강좌 #26] 규제선형 모델 - 릿지, 라쏘, 엘라스틱넷 (0) | 2021.07.03 |
| 머신러닝 강좌 #25] 다항 회귀와 과(대)적합/과소적합 이해 (0) | 2021.06.30 |
| 머신러닝 강좌 #24] 사이킷런 LinearRegression을 이용한 보스턴 주택 가격 예측 (0) | 2021.06.23 |
| 머신러닝 강좌 #22] SMOTE, LightGBM을 이용한 예측 분류 실습 - 캐글 신용카드 사기 검출 (0) | 2021.06.20 |
| 머신러닝 강좌 #21] 분류 XGBoost를 이용한 고객 만족 예측 (0) | 2021.06.17 |
| 머신러닝 강좌 #20] LightGBM에 대한 이해 (0) | 2021.06.14 |
| 머신러닝 강좌 #19] XGBoost (eXtra Boost Machine), Scikit Wrapper Class (0) | 2021.06.11 |



