4.가중치 규제 추가에 대해 : L1규제, L2규제, 드롭아웃 / 정리하기

L1규제, L2규제

 

어떤 훈련 네트워크 구조가 주어졌을 때 데이터를 설명할 수 있는 가중치 값의 집합은 여러 개(여러 개의 모델)입니다. 간단한 모델이 복잡한 모델보다 덜 과대적합될 가능성이 높습니다.

 

간단한 모델이라 함은 파라미터 값 분포의 엔트로피가 작은 모델이나 적은 수의 파라미터를 가진 모델입니다. 그러므로 과대적합을 완화하기 위한 일반적인 방법은 네트워크의 복잡도에 제한을 두어 가중치가 작은 값을 가지도록 강제하는 것입니다. 가중치 값의 분포가 더 균일하게 됩니다. 이를 가중치 규제(weight regularization)라고 하며, 네트워크의 손실 함수에 큰 가중치에 연관된 비용을 추가합니다. 두 가지 형태의 비용이 있습니다.

 

• L1규제: 가중치의 절댓값에 비례하는 비용이 추가됩니다.
• L2규제: 가중치의 제곱에 비례하는 비용이 추가됩니다. L2규제는 신경망에서 가중치 감쇠(weight decay)라고도 부릅니다.

 

from keras import regularizers

model = models.Sequential()
model.add(layers.Dense(16, kernel_regularizer=regularizers.l2(0.001),
                       activation='relu', input_shape=(10000,)))
model.add(layers.Dense(16, kernel_regularizer=regularizers.l2(0.001),
                       activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))

l2(0.001)는 가중치 행렬의 모든 원소를 제곱하고 0.001을 곱하여 네트워크의 전체 손실에 더해진다는 의미입니다. 이 페널티(penalty)항은 훈련할 때만 추가됩니다. 이 네트워크의 손실은 테스트보다 훈련할 때 더 높을 것입니다.

 

확실하게 L2 규제 페널티의 효과를 볼 수 있습니다. 과대적합에 잘 견디고 있습니다.

 

from keras import regularizers

regularizers.l1(0.001)

regularizers.l1_l2(l1=0.001, l2=0.001)

 

---

드롭아웃 추가

드롭아웃(dropout)은 신경망을 위해 사용되는 규제 기법 중에서 가장 효과적이고 널리 사용되는 방법 중 하나입니다. 네트워크 층에 드롭아웃을 적용하면 훈련하는 동안 무작위로 층의 일부 출력 특성을 제외시킵니다.

 

한 층이 정상적으로 훈련하는 동안에는 어떤 입력 샘플에 대해 [0.2, 0.5, 1.3, 0.8, 1.1]벡터를 출력한다고 가정합시다. 드롭아웃을 적용하면 이 벡터의 일부가 무작위로 0으로 바뀝니다. 예를 들어 [0, 0.5, 1.3, 0, .1]이 됩니다. 드롭아웃 비율은 0이 될 특성의 비율입니다. 

 

테스트 단계에서는 어떤 유닛도 드롭아웃되지 않습니다. 그 대신에 층의 출력을 드롭아웃 비율에 비례하여 줄여 줍니다. 훈련할 때보다 더 많은 유닛이 활성화되기 때문입니다.

 

 

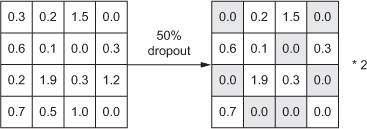
기법이 이상하고 무계획적으로 보일 수 있습니다. 왜 드롭아웃이 과대적합을 줄이는 데 도움이 될까요? 각 샘플에 대해 뉴런의 일부를 무작위하게 제거하면 뉴런의 부정한 협업을 방지하고 결국 과대적합을 감쇠킨다는 것을 깨달았습니다. 

 

핵심 아이디어는 층의 출력 값에 노이즈를 추가하여 중요하지 않은 우연한 패턴을 깨뜨리는 것입니다. 노이즈가 없다면 네트워크가 이 패턴을 기억하기 시작할 것입니다.

 

model = models.Sequential()
model.add(layers.Dense(16, activation='relu', input_shape=(10000,)))
model.add(layers.Dropout(0.5))
model.add(layers.Dense(16, activation='relu'))
model.add(layers.Dropout(0.5))
model.add(layers.Dense(1, activation='sigmoid'))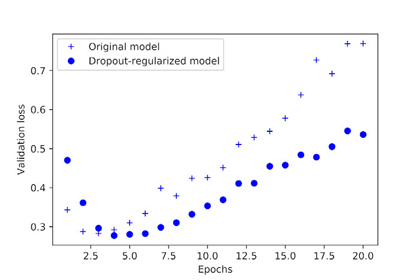

 

---

마지막 정리

• 마지막 층의 활성화 함수: 네트워크의 출력에 필요한 제한을 가합니다. 예를 들어 IMDB분류 예는 마지막 층에 시그모이드 함수를 사용합니다. 회귀 예에서는 마지막 층에 활성화 함수를 사용하지 않습니다.
• 손실 함수: 풀려고 하는 문제의 종류에 적합해야 합니다. 예를 들어 IMDB 예제는 binary_crossentropy를 사용하고, 회귀 예제는 mse를 사용하는 식입니다.
• 최적화 설정: 어떤 옵티마이저를 사용하나요? 학습률은 얼마인가요? 대부분의 경우 rmsprop과 기본 학습률을 사용하는 것이 무난합니다.

손실 함수의 선택에 대해서 언급할 것은 주어진 문제의 성공 지표를 직접 최적화하는 것이 항상 가능하지 않다는 점입니다. 때로는 이 지표를 손실 함수로 바꿀 수 있는 방법이 없습니다. 무엇보다도 손실 함수는 주어진 미니 배치 데이터에서 계산 가능해야 하고(이상적으로는 손실 함수는 하나의 데이터 포인트에서도 계산 가능해야 합니다.) 미분 가능해야 합니다(그렇지 않으면 역전파 알고리즘을 사용하여 네트워크를 훈련시킬 수 없습니다). 예를 들어 널리 사용되는 분류 지표인 ROC AUC는 직접 최적화될 수 없습니다. 그래서 분류 작업에는 크로스엔트로피처럼 ROC AUC를 대신할 지표를 최적화하는 것이 보통입니다. 일반적으로 크로스엔트로피가 낮을수록 ROC AUC가 높다고 기대할 수 있습니다.

 

문제 유형	마지막 층의 활성화 함수	손실 함수
이진 분류	시그모이드	binary_crossentropy
단일 레이블 다중 분류	소프트맥스	categorical_crossentropy
다중 레이블 다중 분류	시그모이드	binary_crossentropy
임의 값에 대한 회귀	없음	mse
0과 1사이 값에 대한 회귀	시그모이드	mse 또는 binary_crossentropy

 

얼마나 큰 모델을 만들어야 하는지 알기 위해서는 과대적합된 모델을 만들어야 합니다. 이는 아주 쉽습니다.

1. 층을 추가합니다.

2. 층의 크기를 키웁니다.

3. 더 많은 에포크 동안 훈련합니다.

 

 

모델 규제와 하이퍼파라미터 튜닝

이 단계가 대부분의 시간을 차지합니다.

• 드롭아웃을 추가합니다.
• 층을 추가하거나 제거해서 다른 구조를 시도해 봅니다.
• L1이나 L2또는 두 가지 모두 추가합니다.
• 최적의 설정을 찾기 위해 하이퍼파라미터를 바꾸어 시도해 봅니다.
• 선택적으로 특성 공학을 시도해 봅니다. 새로운 특성을 추가하거나 유용하지 않을 것 같은 특성을 제거합니다.

 

검증 과정에서 얻은 피드백을 사용하여 모델을 튜닝할 때마다 검증 과정에 대한 정보를 모델에 누설하고 있다는 것입니다. 몇 번만 반복하는 것은 큰 문제가 되지 않습니다. 하지만 많이 반복하게 되면 결국 모델이 검증 과정에 과대적합될 것입니다(모델이 검증 데이터에서 전혀 훈련되지 않는데도 말입니다). 이는 검증 과정의 신뢰도를 감소시킵니다.

 

만족할 만한 모델 설정을 얻었다면 가용한 모든 데이터(훈련 데이터와 검증 데이터)를 사용해서 제품에 투입할 최종 모델을 훈련시킵니다. 그리고 마지막에 딱 한 번 테스트 세트에서 평가합니다. 테스트 세트의 성능이 검증 데이터에서 측정한 것보다 많이 나쁘다면, 검증 과정에 전혀 신뢰성이 없거나 모델의 하이퍼파라미터를 튜닝하는 동안 검증 데이터에 과대적합된 것입니다. 이런 경우에는 좀 더 신뢰할 만한 평가 방법으로 바꾸는 것이 좋습니다.